평균변화율과 미분계수 - 이차함수

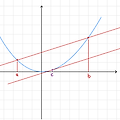
이차함수에서의 평균변화율과 미분계수 이차함수 $f(x)=px^2+qx+c$에서 미분계수가 평균변화율과 같은 지점 $c=\frac{a+b}{2}$ (a와 b의 평균 지점) [증명] $f(x)=px^2+qx+c, f'(x)=2px+q$ $\frac{(pb^2+qb+c)-(pa^2+qa+c)}{b-a}$ $\frac{p(b^2-a^2)-q(b-a)}{b-a}$ $p(b+a)+q=2pc+q$ $2c=a+b$ $c=\frac{a+b}{2}$ ▷ 어떤 이차함수던지 상관없이 항상 성립함!

• format_list_bulleted Math
• · 2021. 8. 29.
• textsms

미분계수와 도함수 (3) - 도함수, 미분법의 공식, 곱의 미분법

도함수 $y=f(x)$ 위의 임의의 점 $(x,f(x))$에서의 접선의 기울기에 대응하는 함수 ▶ 도함수 (기울기 함수) ▶ $f'(x)$ ▶ $y'$ ▶ $\frac{df(x)}{dx}$ 더보기 ▶ 함수 y=f(x)가 정의역에 속하는 모든 x에서 미분가능할 때, 정의역의 각 원소 x에 미분계수 f'(x)를 대응시키면 얻을 수 있는 함수를 y=f(x)의 도함수라 하며, f'(x)로 나타낸다. 도함수의 정의식 1가지! (⚡️암기) ⭐️⭐️ $f'(x)=\lim_{h \rightarrow 0}\frac{f(x+h)-f(x)}{h}$ ⭐️⭐️ (h 대신 $\Delta x$로 표현하기도 함) 다른 표현 방법: $\lim_{\Delta x \rightarrow 0}\frac{\Delta y}{\Delta x}=\..

• format_list_bulleted Math
• · 2021. 8. 28.
• textsms

미분계수와 도함수 (2) - 미분가능성과 연속성

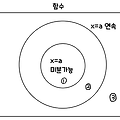
미분계수와 도함수 (1)편 미분계수와 도함수 (1) - 평균변화율과 순간변화율, 미분계수 평균변화율 & 순간변화율 증분 ($\Delta$) (구간 [a, x]에서의 증분) x값의 변화량 x-a를 x의 증분, y값의 변화량 f(x)-f(a)를 y의 증분이라 하고, 각각 $\Delta x,\ \Delta y$와 같이 나타낸다. 평균변화율 함수.. blog.scian.io 미분가능성과 연속성 함수 $f(x)$의 x=a에서의 미분계수 $f^\prime (a)$가 존재할 때, 함수 $f(x)$는 x=a에서 미분가능하다. x=a에서 y=f(x)는 미분가능하다 → $f^\prime (a)$가 존재한다!! → 우미분계수($f^\prime (a)$의 우극한)와 좌미분계수($f^\prime (a)$의 좌극한)가 일치한다...

• format_list_bulleted Math
• · 2021. 8. 28.
• textsms

미분계수와 도함수 (1) - 평균변화율과 순간변화율, 미분계수

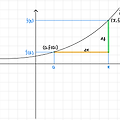
평균변화율 & 순간변화율 증분 ($\Delta$) (구간 [a, x]에서의 증분) x값의 변화량 x-a를 x의 증분, y값의 변화량 f(x)-f(a)를 y의 증분이라 하고, 각각 $\Delta x,\ \Delta y$와 같이 나타낸다. 평균변화율 함수 y=f(x)에서 x의 값이 a에서 x까지 변할 때의 평균변화율: $\frac{\Delta y}{\Delta x}=\frac{f(x)-f(a)}{x-a}=\frac{f(a+\Delta x)-f(a)}{\Delta x}$ = $\overleftrightarrow{AP}$의 기울기 (평균변화율의 기하적 정의) 순간변화율 순간변화율: $f^\prime (a)=\lim_{\Delta x \rightarrow 0}\frac{\Delta y}{\Delta x}=\lim..

• format_list_bulleted Math
• · 2021. 8. 28.
• textsms

Desmos 그래프 그리기

www.desmos.com/calculator?lang=ko Desmos | 그래핑 계산기 www.desmos.com

• format_list_bulleted Math
• · 2021. 8. 20.
• textsms

함수의 연속

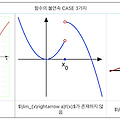
함수의 연속과 불연속 다음 조건을 모두 만족 시킬 때, $f(x)$는 $x=a$에서 연속이라 한다. [1] 함수 $f(x)$는 $x=a$에서 정의되어 있다. [2] 극한값 $\lim_{x\rightarrow a}f(x)$가 존재한다. [3] $\lim_{x\rightarrow a}f(x)=f(a)$ ⭐️ $f(x)$가 $x=a$에서 연속일 조건 정리 (암기!) ⭐️ ▶ 함수값과 극한값이 존재하고, 일치한다. ▶ $\lim_{x\rightarrow a+}f(x)=\lim_{x\rightarrow a-}f(x)=f(a)$ 편하게 생각해 보자면, 그래프를 연필로 그릴 때 연필을 떼지 않고 그래프를 쭉 그릴 수 있으면 연속, 연필을 떼야 하면 불연속으로 생각해 볼 수 있다. ($x=a$에서 그래프가 이어져 있으..

• format_list_bulleted Math
• · 2021. 8. 20.
• textsms