도함수의 활용 III

본 포스팅은 쎈닷컴 김재은 선생님의 수학II 강좌를 바탕으로 작성했음을 밝힙니다. 방정식에의 활용 방정식의 실근의 개수 1️⃣ $f(x)=0$의 서로 다른 실근의 개수 $f(x)=0$의 실근 → $\begin{cases}y=f(x)\\y=0\end{cases}$의 교점의 x좌표 → $y=f(x)$의 x절편 ⭐️ $y=f(x)$의 x절편의 개수 ($f(x)$의 그래프와 x축의 교점의 개수) 2️⃣ $f(x)=g(x)$의 서로 다른 실근의 개수 $f(x)=g(x)$의 실근 → $\begin{cases}y=f(x)\\y=g(x)\end{cases}$의 교점의 x좌표 → $\begin{cases}y=f(x)-g(x)\\y=0\end{cases}$의 교점의 x좌표 → $y=f(x)-g(x)$의 x절편 삼차방정식의..

• format_list_bulleted 🏫 Study/Math
• · 2021. 9. 12.
• textsms

사차함수가 극댓값 또는 극솟값을 가질 조건

본 포스팅은 쎈닷컴 김재은 선생님의 수학I 강좌를 바탕으로 작성했음을 밝힙니다. 참고: 삼차함수가 극값을 가질 조건 삼차함수가 극값을 가질 조건 본 포스팅은 쎈닷컴 김재은 선생님의 수학I 강좌를 바탕으로 작성했음을 밝힙니다. $f(x)=ax^3+bx^2+cx+d$ (a>0)의 그래프의 개형 → $f'(x)=3ax^2+2bx+c$ f'(x)=0의 실근의 개수가 그래프의 개형&극값에 영향 D: blog.scian.io $f(x)=ax^4+bx^3+cx^2+dx+e$ (a>0)의 그래프의 개형 f'(x)=0의 실근의 개수가 그래프의 개형&극값에 영향 📚 f'(x)=0의 실근의 개수 1️⃣ 서로 다른 세 실근 ex) f'(x)=(x-1)(x-2)(x-3) : 극댓값 1개, 극솟값 2개 (a>0) / 극댓값 2개..

• format_list_bulleted 🏫 Study/Math
• · 2021. 9. 8.
• textsms

삼차함수가 극값을 가질 조건

본 포스팅은 쎈닷컴 김재은 선생님의 수학I 강좌를 바탕으로 작성했음을 밝힙니다. $f(x)=ax^3+bx^2+cx+d$ (a>0)의 그래프의 개형 → $f'(x)=3ax^2+2bx+c$ f'(x)=0의 실근의 개수가 그래프의 개형&극값에 영향 D: f'(x)의 판별식 1️⃣ 서로 다른 두 실근 $D/4=b^2-3ac>0$ : 극값을 갖는다. 2️⃣ 중근 $D/4=b^2-3ac=0$ : 극값을 갖지 않는다. (a>0일 때 계속 올라감, a

• format_list_bulleted 🏫 Study/Math
• · 2021. 9. 8.
• textsms

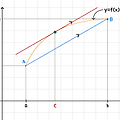
f(x)=f(-x)가 성립한다

f(x)=f(-x)가 성립한다. ↔ f(x)는 우함수이다. ↔ f(x)는 y축 대칭이다. ↔ f(x)는 짝수차 함수 (또는 상수항)이다.

• format_list_bulleted 🏫 Study/Math
• · 2021. 9. 6.
• textsms

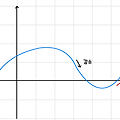
도함수의 활용 II (1) - 함수의 증가와 감소, 함수의 극대와 극소, 극값

함수의 증가와 감소 함수 f(x)가 어떤 구간에 속하는 임의의 두 수 $x_1, x_2$에 대하여 $x_1

• format_list_bulleted 🏫 Study/Math
• · 2021. 9. 3.
• textsms

도함수의 활용 I (2) - 롤의 정리, 평균값 정리

도함수의 활용 I (1) 편 도함수의 활용 I (1) - 접선의 방정식 접선의 방정식 접선의 기울기 곡선 $f(x)$ 위의 점 $P(a, f(a))에서의 접선의 기울기는 x=a에서의 미분계수 $f'(a)$와 같다. 접선의 개수 = 접점의 개수 = 접점의 x좌표의 개수 접선의 방정식 📚Background blog.scian.io 고등 수학 II에서 나오는 4가지 정리 최대·최소 정리 사잇값 정리 롤의 정리 평균값 정리 * 최대·최소 정리와 사잇값 정리는 아래 글 참고: 2021.08.20 - [♾ 수학/수학 II] - 함수의 연속 함수의 연속 함수의 연속과 불연속 다음 조건을 모두 만족 시킬 때, $f(x)$는 $x=a$에서 연속이라 한다. [1] 함수 $f(x)$는 $x=a$에서 정의되어 있다. [2] ..

• format_list_bulleted 🏫 Study/Math
• · 2021. 8. 31.
• textsms