도함수의 활용 I (1) - 접선의 방정식

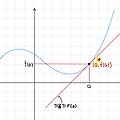
접선의 방정식 접선의 기울기 곡선 $f(x)$ 위의 점 $P(a, f(a))에서의 접선의 기울기는 x=a에서의 미분계수$f'(a)$와 같다. 접선의 개수 = 접점의 개수 = 접점의 x좌표의 개수 접선의 방정식 📚Background 기울기가 m이고,$(x_1,y_1)$을 지나는 직선의 방정식 :$y=m(x-x_1)+y_1$위의 배경지식을 이용하면, 함수 f(x)가 x=a에서 미분가능할 때, 곡선 y=f(x) 위의 점 P(a, f(a))에서의 접선의 방정식 :$y=f'(a)(x-a)+f(a)$(이항하기 전$y-f(a)=f'(a)(x-a)$) 접선의 방정식을 구하는 방법 I. 접점을 주고 구하기$y=f(x)$위의 점$(a,f(a))$에서의 접선의 방정식 구하기 📚Step 1. 접선의 기울기 ..

• format_list_bulleted Math
• · 2021. 8. 31.
• textsms

관계식이 주어질 때 미분계수 구하기

아래 3가지를 구해놓고 문제 풀기! (암기!) [1] f(0) [2] f’(0) → 미분계수의 정의식 [3] f’(x) → 도함수의 정의식

• format_list_bulleted Math
• · 2021. 8. 29.
• textsms

평균변화율과 미분계수 - 이차함수

이차함수에서의 평균변화율과 미분계수 이차함수 $f(x)=px^2+qx+c$에서 미분계수가 평균변화율과 같은 지점 $c=\frac{a+b}{2}$ (a와 b의 평균 지점) [증명] $f(x)=px^2+qx+c, f'(x)=2px+q$ $\frac{(pb^2+qb+c)-(pa^2+qa+c)}{b-a}$ $\frac{p(b^2-a^2)-q(b-a)}{b-a}$ $p(b+a)+q=2pc+q$ $2c=a+b$ $c=\frac{a+b}{2}$ ▷ 어떤 이차함수던지 상관없이 항상 성립함!

• format_list_bulleted Math
• · 2021. 8. 29.
• textsms

함수의 연속

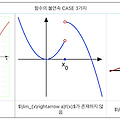
함수의 연속과 불연속 다음 조건을 모두 만족 시킬 때, $f(x)$는 $x=a$에서 연속이라 한다. [1] 함수 $f(x)$는 $x=a$에서 정의되어 있다. [2] 극한값 $\lim_{x\rightarrow a}f(x)$가 존재한다. [3] $\lim_{x\rightarrow a}f(x)=f(a)$ ⭐️ $f(x)$가 $x=a$에서 연속일 조건 정리 (암기!) ⭐️ ▶ 함수값과 극한값이 존재하고, 일치한다. ▶ $\lim_{x\rightarrow a+}f(x)=\lim_{x\rightarrow a-}f(x)=f(a)$ 편하게 생각해 보자면, 그래프를 연필로 그릴 때 연필을 떼지 않고 그래프를 쭉 그릴 수 있으면 연속, 연필을 떼야 하면 불연속으로 생각해 볼 수 있다. ($x=a$에서 그래프가 이어져 있으..

• format_list_bulleted Math
• · 2021. 8. 20.
• textsms

함수의 극한 (4) - 함수의 극한값의 계산 & 미정계수의 결정 & 함수의 극한의 대소 관계

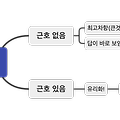
함수의 극한 (3) 편 함수의 극한 (3) - 함수의 극한에 대한 성질 함수의 극한 (2) 편 함수의 극한 (2) - 우극한과 좌극한 함수의 극한 (1)편 함수의 극한 (1) - 함수의 수렴과 발산 함수의 수렴과 발산 함수 $f(x)$에서 $x$의 값이 a가 아니면서 a에 한없이 가까워질 때 blog.scian.io 함수의 극한값의 계산 [1] $\frac{0}{0}$ 꼴의 극한 (0은 숫자 0이 아니라 0에 한없이 가까워지는 것을 나타냄) ▶ 식 변형 (⭐️인수분해 / 유리화(근호가 나올 때) / 통분⭐️ 딱 세가지로 1,2,3번 사용!) ex) $\lim_{x\rightarrow 2}\frac{x^2-4}{x-2}=\lim_{x\rightarrow 2}x+2$=4 [2] $\frac{\pm\infty..

• format_list_bulleted Math
• · 2021. 8. 18.
• textsms

함수의 극한 (3) - 함수의 극한에 대한 성질

함수의 극한 (2) 편 함수의 극한 (2) - 우극한과 좌극한 함수의 극한 (1)편 함수의 극한 (1) - 함수의 수렴과 발산 함수의 수렴과 발산 함수 $f(x)$에서 $x$의 값이 a가 아니면서 a에 한없이 가까워질 때($x\rightarrow a$) $f(x)$의 값이 일정한 값 L에 한없이 가 blog.scian.io 함수의 극한에 대한 성질 ⭐️⭐️⭐️⭐️ 극한값 $\lim_{x \rightarrow a}f(x)$, $\lim_{x \rightarrow a}g(x)$가 존재할 때, ⭐️⭐️⭐️⭐️ 사칙 연산이 가능! * 전제가 중요!! [1] $\lim_{x \rightarrow a}cf(x)=c\lim_{x \rightarrow a}f(x)$ [2] $\lim_{x \rightarrow a}\{..

• format_list_bulleted Math
• · 2021. 8. 18.
• textsms