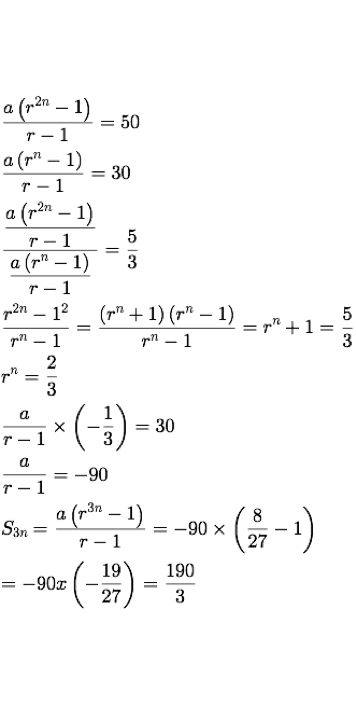부분의 합이 주어진 등비수열

ex)

등비수열 ${a_n}$의 첫째항부터 제n항까지의 합 $S_n$에 대하여 $S_n=30, S_{2n}=50$일 때, $S_{3n}$의 값을 구하시오.

- 쎈 수학 I / 146p 970번 문제

$\begin{aligned}\dfrac{a\left( r^{2n}-1\right) }{r-1}=50\\ \dfrac{a\left( r^{n}-1\right) }{r-1}=30\\ \dfrac{\dfrac{a\left( r^{2n}-1\right) }{r-1}}{\dfrac{a\left( r^{n}-1\right) }{r-1}}=\dfrac{5}{3}\\ \dfrac{r^{2n}-1^{2}}{r^{n}-1}=\dfrac{\left( r^{n}+1\right) \left( r^{n}-1\right) }{r^{n}-1}=r^{n}+1=\dfrac{5}{3}\\ r^{n}=\dfrac{2}{3}\\ \dfrac{a}{r-1}\times \left( -\dfrac{1}{3}\right) =30\\ \dfrac{a}{r-1}=-90\\ S_{3n}=\dfrac{a\left( r^{3n}-1\right) }{r-1}=-90\times \left( \dfrac{8}{27}-1\right) \\ =-90x\left( -\dfrac{19}{27}\right) =\dfrac{190}{3}\end{aligned}$