도함수의 활용 II (2) - 함수의 그래프와 함수의 최대·최소

본 포스팅은 쎈닷컴 김재은 선생님의 수학II 강좌를 바탕으로 작성했음을 밝힙니다. 도함수의 활용 II (1) 편 도함수의 활용 II (1) - 함수의 증가와 감소, 함수의 극대와 극소, 극값 함수의 증가와 감소 함수 f(x)가 어떤 구간에 속하는 임의의 두 수 $x_1, x_2$에 대하여 $x_1 1️⃣$f(x_1) 2️⃣ $f(x_1)>f(x_2)$이면 f(x)는 이 구간에서 감소 함수의 증가와 감소의 판정 함수 f(x)가 어떤.. blog.scian.io 함수의 그래프와 함수의 최대·최소 : 1개씩만 존재! (극대, 극소와 헷갈리면 안됨!) f(x)가 [a, b]에서 연속일 때 최댓값, 최솟값 구하기 1️⃣ f'(x)로 그래프의 개형 구하기 * 그래프 개형 그리기: 도함수의 활용 II (1) - 함..

• format_list_bulleted Math
• · 2021. 9. 9.
• textsms

도함수의 활용 I (2) - 롤의 정리, 평균값 정리

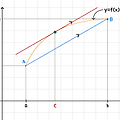
도함수의 활용 I (1) 편 도함수의 활용 I (1) - 접선의 방정식 접선의 방정식 접선의 기울기 곡선 $f(x)$ 위의 점 $P(a, f(a))에서의 접선의 기울기는 x=a에서의 미분계수$f'(a)$와 같다. 접선의 개수 = 접점의 개수 = 접점의 x좌표의 개수 접선의 방정식 📚Background blog.scian.io 고등 수학 II에서 나오는 4가지 정리 최대·최소 정리 사잇값 정리 롤의 정리 평균값 정리 * 최대·최소 정리와 사잇값 정리는 아래 글 참고: 2021.08.20 - [♾ 수학/수학 II] - 함수의 연속 함수의 연속 함수의 연속과 불연속 다음 조건을 모두 만족 시킬 때,$f(x)$는$x=a$에서 연속이라 한다. [1] 함수$f(x)$는$x=a$에서 정의되어 있다. [2] ..

• format_list_bulleted Math
• · 2021. 8. 31.
• textsms

도함수의 활용 I (1) - 접선의 방정식

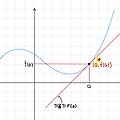
접선의 방정식 접선의 기울기 곡선 $f(x)$ 위의 점 $P(a, f(a))에서의 접선의 기울기는 x=a에서의 미분계수$f'(a)$와 같다. 접선의 개수 = 접점의 개수 = 접점의 x좌표의 개수 접선의 방정식 📚Background 기울기가 m이고,$(x_1,y_1)$을 지나는 직선의 방정식 :$y=m(x-x_1)+y_1$위의 배경지식을 이용하면, 함수 f(x)가 x=a에서 미분가능할 때, 곡선 y=f(x) 위의 점 P(a, f(a))에서의 접선의 방정식 :$y=f'(a)(x-a)+f(a)$(이항하기 전$y-f(a)=f'(a)(x-a)$) 접선의 방정식을 구하는 방법 I. 접점을 주고 구하기$y=f(x)$위의 점$(a,f(a))$에서의 접선의 방정식 구하기 📚Step 1. 접선의 기울기 ..

• format_list_bulleted Math
• · 2021. 8. 31.
• textsms

관계식이 주어질 때 미분계수 구하기

아래 3가지를 구해놓고 문제 풀기! (암기!) [1] f(0) [2] f’(0) → 미분계수의 정의식 [3] f’(x) → 도함수의 정의식

• format_list_bulleted Math
• · 2021. 8. 29.
• textsms

평균변화율과 미분계수 - 이차함수

이차함수에서의 평균변화율과 미분계수 이차함수 $f(x)=px^2+qx+c$에서 미분계수가 평균변화율과 같은 지점 $c=\frac{a+b}{2}$ (a와 b의 평균 지점) [증명] $f(x)=px^2+qx+c, f'(x)=2px+q$ $\frac{(pb^2+qb+c)-(pa^2+qa+c)}{b-a}$ $\frac{p(b^2-a^2)-q(b-a)}{b-a}$ $p(b+a)+q=2pc+q$ $2c=a+b$ $c=\frac{a+b}{2}$ ▷ 어떤 이차함수던지 상관없이 항상 성립함!

• format_list_bulleted Math
• · 2021. 8. 29.
• textsms

미분계수와 도함수 (3) - 도함수, 미분법의 공식, 곱의 미분법

도함수 $y=f(x)$ 위의 임의의 점 $(x,f(x))$에서의 접선의 기울기에 대응하는 함수 ▶ 도함수 (기울기 함수) ▶ $f'(x)$ ▶ $y'$ ▶ $\frac{df(x)}{dx}$ 더보기 ▶ 함수 y=f(x)가 정의역에 속하는 모든 x에서 미분가능할 때, 정의역의 각 원소 x에 미분계수 f'(x)를 대응시키면 얻을 수 있는 함수를 y=f(x)의 도함수라 하며, f'(x)로 나타낸다. 도함수의 정의식 1가지! (⚡️암기) ⭐️⭐️ $f'(x)=\lim_{h \rightarrow 0}\frac{f(x+h)-f(x)}{h}$ ⭐️⭐️ (h 대신 $\Delta x$로 표현하기도 함) 다른 표현 방법: $\lim_{\Delta x \rightarrow 0}\frac{\Delta y}{\Delta x}=\..

• format_list_bulleted Math
• · 2021. 8. 28.
• textsms